Consider this $9\times 9\times 9$ grid, in which some cubes have been shaded.
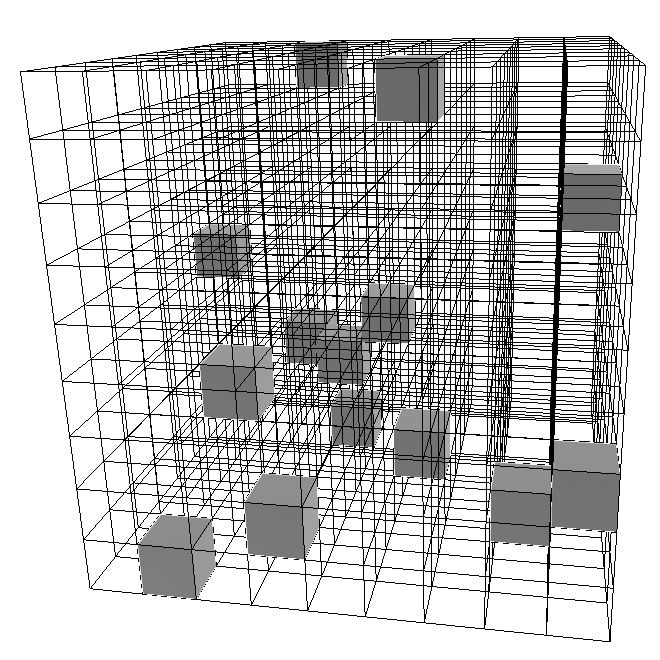
It can be represented in two dimensions by viewing it from one side and using numbers from $1$ to $9$ to give the location of each cube in the into-the-page direction.
Challenge Add cubes to the above grid so that, no matter which side we look at, these numbers obey the rules of Sudoku.
I copied these numbers over to SudokuExchange.com so you can solve it online. Ignore the warning that there may be more than one solution; you have extra information!
Below is a hint to help you if you have trouble dealing with the 3d nature of the puzzle.
Hint
The numbers must form a Sudoku from the side we are currently looking at. The condition that they also form a Sudoku when viewed from the other possible directions is equivalent to demanding that each $3\times 1$ and $1\times 3$ rectangle within the $3\times 3$ blocks contains one number from each of the sets $1$, $2$, $3$; $4$, $5$, $6$ and $7$, $8$, $9$.
Addendum: As far as I know, this Sudoku variant hasn’t been invented before. I did find a site selling 3d-printed models of Sudokus made according to the same scheme. But these only obey the rules of Sudoku when seen from the front or back; not from the other sides. In order to print it they did have the additional requirement that all the blocks are connected, so they had to put in some extra computational effort to get that.

Wow! I Just wake UP and think: why do The algoritim not indicate me a 3d sudoku until now? Does Thay not exist? And here i am… You have to desenvolve this Idea.
I made a 3d sudoku puzzle into an app a few years ago but haven’t released it. It’s actually 27 puzzles in one. Would you like to play it?
That’s actually exactly what I was looking for, is this still around?