Consider this $9\times 9\times 9$ grid, in which some cubes have been shaded.
It can be represented in two dimensions by viewing it from one side and using numbers from $1$ to $9$ to give the location of each cube in the into-the-page direction.
Challenge Add cubes to the above grid so that, no matter which side we look at, these numbers obey the rules of Sudoku. Continue reading
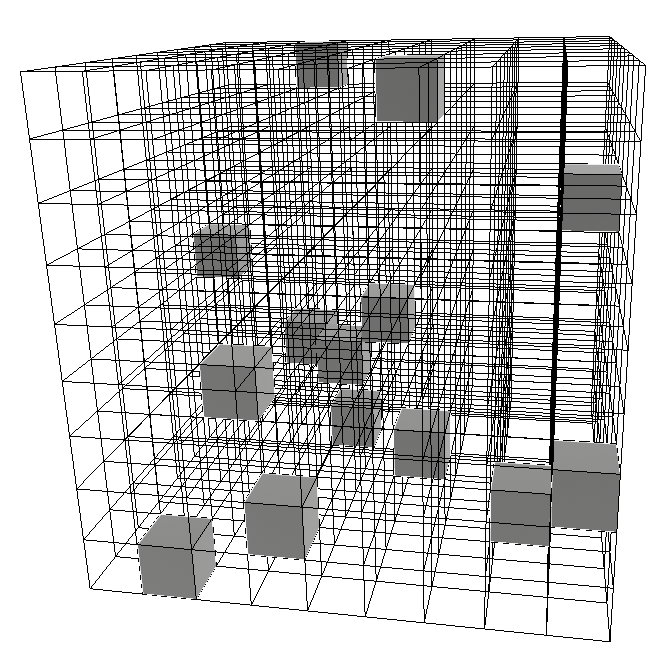
The most recent of Matt Parker’s Maths Puzzles was the unique distancing problem:
For which $n\in\mathbb N$ is it possible to place $n$ counters on an $n\times n$ square grid so that there’s a different distance between each pair of distinct counters? (Distances are measured in the normal Pythagorean way, so if there is a counter at $(0,0)$ we cannot have counters at both $(5,0)$ and $(4,3)$).
For small $n$ the problem is not too hard. I managed to use a computer search to find solutions for $n<8$ and prove that there were no solutions for $8\leq n < 11$. For $n\geq 16$ it’s trivial that there are no solutions because the number of pairs of counters is greater than the number of distances possible on the grid. This leaves the cases $n = 11$, $12$, $13$, $14$ and $15$.
Fellow puzzler Gal Holowitz wrote code efficient enough to deal with four of these remaining cases, $n = 11$, $12$, $13$ and $14$, finding that there were no solutions for any of them. But for the $n=15$ case their code is still running!
So you would think that $n=15$ was the hardest case of all. But in fact you can prove that there are no solutions for this case by using just pen and paper. Here’s how. Continue reading
Real numbers can be represented by decimals or by continued fractions, but both of these systems have the problem that the representations are not unique. This nonuniqueness can introduce ugly complications into proofs that use these representations, in particular those regarding the cardinality of $\mathbb R$.
In this post I’ll explain what causes these complications, and then define a system that avoids them. In particular I’ll define an elegant and order-preserving bijection from the interval $[0,1)$ to the set $\mathbb N \to\mathbb N$ of sequences of natural numbers.
(In case this notation is unfamiliar to readers, the set $[x,y)$ contains all the real numbers from $x$ to $y$, including $x$ but not including $y$. The set $A\to B$ contains all functions from $A$ to $B$. Also, I use the convention that $\mathbb N$ contains $0$.)
There are various ways that we can multiply vectors.
If we wanted to divide by a vector we would need for one of these equations to have a unique inverse. Sadly this rarely happens.
But there are some cases where you can divide by a vector. The case I want to look at today is the one where $V$ is $1$-dimensional. Continue reading
In the last post, I talked about Monads on Monoids. We defined these by turning each monoid into a category (its delooping), and then looking at monads on this category. This data could then be reexpressed in terms of the original monoid.
We can also apply exactly the same process to define adjunctions between monoids. These were studied by Vladimir Molotkov in his paper ‘Adjunction in Monoids‘. Continue reading
This post is inspired by a couple of posts on math.stackexchange.com asking what a ‘monad on a monoid’ is.
In category theory there are a couple of especially simple kinds of category. For any partial order we can put a category structure on its elements by saying that there’s a unique morphism $x\to y$ if $x\leq y$ and none otherwise. And for any monoid we can construct a category with one object and with the morphisms from that object to itself being the elements the monoid.
These two examples are complementary to each other. With partial orders you can have as many objects as you want, but the morphisms have to be as simple as possible. Monoids are the opposite, you can only have one object but it can have as many morphisms as you like.
Sometime when we’re doing category theory it can help to think about these categories as a way of restricting our attention. If we have some complicated categorical construction then we can gain some intuition about it by looking at how it applies to these two simple cases. Today the ‘complicated categorical construction’ we’re interested in is monads. Continue reading
